Micorosoft Small Basic 基本プログラミング学習

      ' 座標と円弧
      '
      Start()

      Sub Start
        GraphicsWindow.Title = "円弧"
        GraphicsWindow.Height = 200
        GraphicsWindow.Width = 200
        GraphicsWindow.Show()
        zahyo()
        aCurve()
      EndSub

      Sub zahyo
        GraphicsWindow.DrawLine(0,0,0,200)
        GraphicsWindow.DrawLine(0,0,200,0)
      EndSub

      Sub aCurve
      For x=0 To 100
        GraphicsWindow.SetPixel(x,Math.SquareRoot(10000-x*x),"red")
      EndFor
          EndSub

    

API is Application Program Interface.

API の例

• LINE API
• Twitter API
• Google Maps API
• YouTube API
• ...

Small Basic のAPI

Small Basic API の参照ページ

このページには、Small Basic のおよそ20個のクラスごとにプロパティとメソッドをまとめてある。

次のスクリーンショットの例は、ネットワークのAPIである。

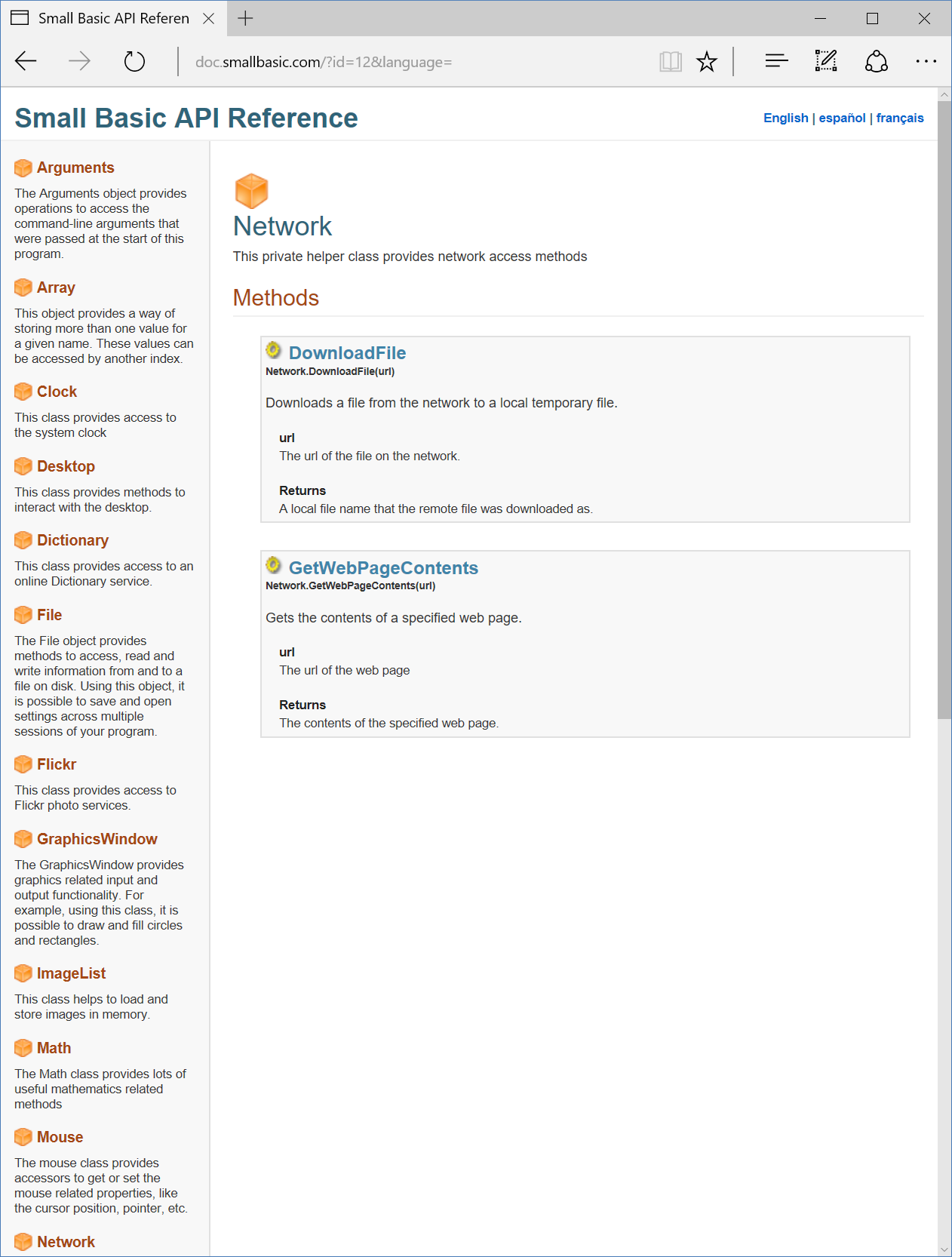
ネットワークには、2つのメソッドがある。というか、2つしかない。ファイルのファウンロードとウェブページのコンテンツ入手の2つのメソッドがある。

ネットワークのプロパティは、ひとつもない。

Small Basic のプログラム ギャラリー

今月の挑戦11月号には、Small Basic の新ロゴを描くや3目ならべなどもある。

Rosetta code にも Small Basic のコードはある。

たとえば、マンデルブロー集合のプログラム。Rosetta code

      GraphicsWindow.BackgroundColor = "Black"
      GraphicsWindow.MouseDown = OnMouseDown

      Sub OnMouseDown
        pic = Flickr.GetRandomPicture("Japan, dogo")
        GraphicsWindow.DrawResizedImage(pic, 0, 0, 640, 480)
      EndSub
       
      
    

写真のキーワードを"Matsuyama"にしてみるとどうだろうか

赤系統

• IndianRed   #CD5C5C
• LightCoral   #F08080
• Salmon   #FA8072
• Red   #FF0000
• DarkRed   #8B0000

ピンク

• Pink #FFC0CB
• DeepPink #FF1493

オレンジ系統

• Coral #FF7F50
• Orange #FFA500

黄色系統

• Gold #FFD700
• Yellow #FFFF00

緑系統

• Lime #00FF00
• Green #008000

青系統

• Aqua #00FFFF
• Cyan #00FFFF
• Turquoise #40E0D0
• SteelBlue #4682B4
• Blue #0000FF

茶系統

• Bisque #FFE4C4
• Tan #D2B48C
• Brown #A52A2A

白系統

• White #FFFFFF
• Snow #FFFAFA
• Azure #F0FFFF
• Beige #F5F5DC

灰色系統

• Gray #808080
• SlateGray #708090
• Black #000000

      a11x1 + a12x2 + ... + a1nxn = b1
      a21x1 + a22x2 + ... + a2nxn = b2

      ...

      an1x1 + an2x2 + ... + annxn = bn
    

ガウス消去法

ロゼッタコードには、Small Basic のコードがなかった。自分で書いてみたがうまく動かないようだ。修正がいる。下のコードは、SBのエディタからコピーいたためインデントされていない。

空白についてあるいはSpace (punctuation)

PowerShellでコードを書いたすごいひともいるようだ。

      '連立一次方程式

      Sub yomu
      n=3
      a[1][1]=2
      a[1][2]=9
      a[1][3]=4
      a[1][4]=1
      a[2][1]=7
      a[2][2]=5
      a[2][3]=3
      a[2][4]=2
      a[3][1]=6
      a[3][2]=1
      a[3][3]=8
      a[3][4]=3
      EndSub

      Sub toku
      For i=1 To n
      pivot = a[i][i]
      For j=1 To n+1
      a[i][j]=a[i][j]/pivot
      For j=1 To n
      If (j=1) Then
      goto loop
      endif
      pivot1=a[j][i]
      For k=1 To n+1
      a[j][k]=a[j][k]-a[i][k]*pivot1
      loop:
      EndFor
      EndFor
      EndFor
      EndFor
      For i=1 To n
      X[i]=a[i][n+1]
      EndFor
      EndSub

      Sub utu
      For i=1 To n
      TextWindow.Write("X(" + i +")=")
      TextWindow.WriteLine(X[i])
      EndFor
      EndSub

      yomu()
      toku()
      utu()

    

宇宙船は、地球の中心と月の中心とを通る平面内で航行するものとする。また、軌道修正はしない。宇宙船に引力をおよぼす天体は、地球と月だけとする。また、地球と月は空間に固定する。

地球を原点とし、月の方向をX軸とする平面座標を考える。

      (0,0)    地球の位置
      (C,0)    月の位置
      C        地球と月の距離 = 3.844 ⋅ 105km
      (x,y)    宇宙船の位置
      r        地球と宇宙船の距離
      s        月と宇宙船の距離
      (Vx, Vy)   宇宙船の速度
      (αx, αy)    宇宙船の加速度
      (ƒx, ƒy)     宇宙船に働く力
      mE     地球の質量  = 5.977 ⋅ 1024kg
      mM     月の質量  = 7.352 ⋅ 1022kg
      m        宇宙船の質量 = 1000kg とする
      G        万有引力定数 = 6.673 ⋅ 10-11 m3kg-1sec-2
      t        時刻
    

       Vx=dx/dt
       Vy=dy/dt

       αx=dvx/dt
       αy=dvy/dt

       ƒx=m αx
       ƒy=m αy

       r=√ x2 + y2

       s=√ (x-C)2 + y2

       ƒx = - GmE ⋅ m / r2 ⋅ (x/r) - GmM ⋅ m / s2 ⋅ (x-C)/s 

       ƒy = - GmE ⋅ m / r2 ⋅ y/r - GmM ⋅ m / s2 ⋅ y/s 

      
    

時間dtを十分に小さくとれば、dt時間後の宇宙船の位置と速度は、

	(x+Vx ⋅ dt, y+Vy ⋅ dt)
	(Vx+αx ⋅ dt, Vy+αy ⋅ dt)
      

で求まる。