Forthはプログラム言語です。しかし、世の中で良く使われているC言語 やJavaなどとは違うスタイルの言語です。あまり表には顔を出さないタイプ の言語です。隠れ言語かもしれません。歴史はそれほど古くはありません が、1970年にチャールズ・ムーアによってスタックという記憶装置の仕組み を中心に考案された言語です。
多数のプログラム言語は、それぞれの標準規格が各国で定められている。 日本では、JIS「日本工業規格」のX(情報処理)分野で「プログラム言語/ 図形・文書処理・文書交換/OSI・LAN・データ通信/出力機器・記 録媒体」が定められている。
現実には、プログラム言語開発の中心になっているアメリカの規格(ANSI)が優先していることが多い。
Forth は、特に実際に動作する処理系が限られかつ、ユーザも限られているた めこの傾向が強い。
Jupiter ACE
Jupiter ACE は、1982年にイギリスのJupiter Cantab Ltd が発売した8 ビットの Z80Aマイクロプロセッサを使用したパーソナルコンピュータだった。初期 のマイコンはプログラム言語としてBASICを装備するのがふつうだったが、 ACEは 珍しくForth言語を使っていた。
ACEの名前の由来は、イギリスが1950年に開発した Pilot ACE (Automatic Computing Engine)にあるという。
筆者も実際に Jupiter ACEをiPadにインストールしてみたが、1982年当 時のマイコンのキーボードを画面に表示して iPad標準のキーボードではな く ACEの環境でForthを実行できるようになっている。当時を知っている人 間にとっては、とても懐かしい画面であり、初心者も1980年代のパソコンを 体験できる。しかし、ACEとForceの両方に興味がないと使いこなすようにな るのは無理なような気がした。
また、筆者がテストしてうまく動いたのは、古い型のiPadでだった。最 新のiPad Proでは、入力は問題なくできるが、式を評価した結果が画面に出力されなかった。原因は、まだ不明である。
gforth
Win32forth
gforth
Windows版は、 Home of Gforthのなかにある 「Win32 self installing」の説明があるファイ ルを探し出してダウンロードしたあと、そのダウンロードファイルを実行する。
最新版のソースファイルは、Git レポジトリーにある。
The Home of the Win32Forth Project Group
最新の版はSourceforgeにあるが、Win32forthは、そのシステム固有の性 質から、アンチウイルスソフトがインストールを拒否する。そのためシステ ムの内部に詳しい人にしかすすめることができない。何か問題を引き起すかもし れない。
以下、その他のForthコンパイラ。
大文字、小文字はどちらでもかまわない。区別されない。
アイコンをクリックする、またはターミナルで次のようにタイプする。
gforth
bye
2 17 + .
数、記号の間に空白をひとつ以上タイプしEnterキーを押す。この場合は、 「2」「17」「+」「.」の間に空白を入れ、Enterキー。
Forth は、この入力された数、記号を上から順にスタックとよばれるメモリに下方へと押し込み、それを「解釈」し、「実行」し、その「結果を画面に表示」する。
17
2
スタックの初期状態は「空」である。Forthは「2 17 + .」が入力されると、 左から順に空白で区切った数や記号をスタックへ上から下へ押し下げて格納 する。Forthは、入力された文字列を「ワード」、「数」、「未定義」の3通 りに解釈する。ここでワードは、すでに定義された手続を意味するForth 言語での用語である。
「2 17 + .」をForthがどのように処理するかをみてみよう。
まず、最初の文字列「2」がワードかどうか「ディクショナリー」の中に あるか調べる。「2」はディクショナリーの中にはないことがわかる。次 に「2」が数字の条件にあっているかどうか調べる。結果、「2」は数(か ず)であることがわかり、スタックの最上位(TOS、トップオブスタック)に「プッシュ」される。
「17」も同様にして、数としてスタックにプッシュされる。この時、スタッ クの一番上にあった 2 は、押し下げられる。スタックは、上から17、2とな る。
入力された文字列の次「+」をForthは、ディクショナリーにあるワード のなかの加算演算子として処理する。「+」ワードは、2と17を加えスタッ クに「19」を残す。
ワード「.」(ドットと発音する)は、19をスタックから取り除き、画面に 表示する。
Forthは、入力の解釈と実行がおわると「ok」を画面にだす。
もしも、ディクショナリーにないワードが入力されると「Undefined word」のエラーを出力する。
X
Human
THING
17 23 - . -6 ok
5 7 * . 35 ok
365 7 / . 52 ok
「.s」のあとEnterキーで、スタックの中にある数が<個数>をはじめに、 スタックの下から順に、左から右へ画面に出力される。
52 7
.s
*
.s
.
.s
ディクショナリーに新しいワードを登録する。
「:」と「;」で囲む。「:」(コロン)が新しいワード定義のはじまり、「;」 (セミコロン)がおわりを示す。
次の例は、「*+」という新しいワードを定義する。
: *+ * + ;
次の結果は、どうなる?
: *+ * + ;
5 6 7 *+ .
see *+
Forthには、see というワードがある。これを使えば、*+ という自分が定義 したワードのなかを見ることができる。これを逆コンパイルという。
Forthのなかの動作を理解するために see は便利なワードである。
現代のコンピュータのあらゆるCPUはすべてスタックを利用するように設計されてい る。CPUの設計をアーキテクチャという。したがって、Forthプログラムはこの スタック操作を利用できることからCPUを効率的に使うプログラムを書くこと ができるといえる。
では、スタックとはどんなものか?
次の行を入力してみよう。「Enterキー」は、コンピュータ・キーボード のEnterと刻印されたキーを押す。スマートフォンでは、画面上の仮想キー ボードの右端あたりに改行印がついたキーである。
2 5 73 -16 「Enterキー」 ok
これを入力するとスタックは次のようになる。
セル# コンテンツ
0 -16 (TOS = Top of stack)
1 73 (NOS = Next on stack)
2 5
3 2
Forthでは、データ構造をゼロから順に数える。したがって、TOSは、#0、 NOSは、#1 ...となる。
では、さきほどの「2 5 73 -16」行を入力したあと、次の行を入力して みよう。
+ - * . 「Enterキー」
「xxx」は、いくつになるか?
+ - * . xxx ok
セル# 初期値 + - * .
0 -16 57 -52 -104 空
1 73 5 2
2 5 2
3 2
最後の「.」は画面に「-104」を表示し、スタックを空にする。したがっ て、xxx は、-104である。
スタック操作の基本
セル | 初期値 | DROP SWAP ROT DUP
0 | -16 | 73 73 5 -16
1 | 73 | 5 -16 -16 -16
2 | 5 | 2 5 73 73
3 | 2 | 2 2 5
4 | | 2
もう一つのスタック基本操作
pick と roll は、整数を前につけて下のように3 pickや、3 rollのように スタックのどのセルをpickしたり、rollするか指定して使う。
セル | 初期値 | OVER TUCK 3 PICK 3 ROLL
0 | -16 | 73 -16 2 2
1 | 73 | -16 73 -16 -16
2 | 5 | 73 -16 73 73
3 | 2 | 5 5 5 5
4 | | 2 2 2
o pick は、dupと同じ、1 pick は、over、1 roll は、swapと同じで 2roll は rot になる。
ソース・プログラム(例 mysource.fs)を読み込むには2つの方法がある。
include mysource.fs
s" mysource.fs" included
これまでスタックは一つしか取り扱ってこなかった。しかし、実際には二つあ る。ひとつは「パラメータ(データ) スタック」、もうひとつは「リターン ス タック」である。Forthプログラムでは、「パラメータ(データ) スタック」の 方がよく利用されるため、スタックというときは普通こちらをさしている。
パラメータという謂れは、ワードからワードへわたされるデータ(パラメータ、 引数)であることによる。
普段は、Forthの普通のパラメータスタックを使い、それでは足りなくなったときにリ ターンスタックを使うようなプログラムをすることができる。
新しくワードを定義してコンパイルすると、その新しいワードをつくるために 呼び出された既にあるワードへのリンクが生成される。
このリンク機構は、リターンスタック(rstack)と呼ばれる。
リンクは入れ子(ネスト)構造になることがある。すなわち、再帰的呼び 出しのとき、戻りのアドレスをスタックに格納する。
数をリターンスタック(rstack)に収納するときは、>r 。rstackから取り出す ときは、r>。ワード r@は、rstackのトップをTOSにコピーする。
何故、わざわざrstackを使うかの理由は、実はプログラムをデータスタックだ けで書くと非常に複雑になってしまうことにある。
もうひとつ、ふつうのプログラミングには欠かせない変数を使うこともできる。 というか、変数を使わなければスタックだけのプログラミングでは複雑になっ てしまう場合があるからである。
変数とは、名前をつけた記憶場所で、数を収納するためのものであるの は、ふつうのプログラム言語と同じ。
「variable x」は、記憶装置のなかのある場所に「x」という名前をつけ る。「!」(ストア)は、数とアドレスをもとにそのアドレスに数を収納する。 「@」(フェッチ)は、アドレスからその中味をTOSに入れる。
次の例を実行してみる。
variable x
3 x !
x @ .
「x .」を実行するとある数字がでる。それが変数xのアドレスである。
13 value thirteen thirteen .
47 to thirteen
: v+ ( a b c d -- a+c b+d) locals| d c b a | a c + b d + ; 2 3 4 5 v+ .s [2] 6 8 ok
新しくワード hi を次のような書式で定義してみよう。「hi」 は、「.” こんにち は!”」を定義した名前である。「ドット(.)」「ダブルクオーテーション(2重引用 符)」「スペース」の3つの文字と最後の「ダブルクオーテーション」に囲まれ た文字列が画面に表示される。(注)「こんにちは」は全角平仮名であるが、ドッ ト、ダブルクオーテーション、スペースは、全部半角アスキー文字にすること に注意。
まず、ドット、ダブルクオートの次には必ず半角文字を入れることを忘れない ようにして、文字列表示ができることを試してみよう。
." こんにちは!"
うまくいったら、次のように新しいワード「hi」とその定義内容 「." こんにちは!"」を並べて前後を「:」コロンと「;」セミコロンでは さみ入力する。これで hi が定義された。
: hi ." こんにちは!" ;
「.”」は、次の「”」がくるまでの文字列を表示する。
新しいワード hi は何度でも呼び出せる。
hi hi
space 空白(半角スペース)
12 spaces 12個の空白
42 emit * (アスタリスク)
cr 改行
記号、数字、アルファベットは、次の表のようになっている。アルファベット 大文字Aに対応するコードは、60列の5行だから、65となる。アスタリスクは、 42だから、42 emit で画面にアスタリスクが1個表示される。
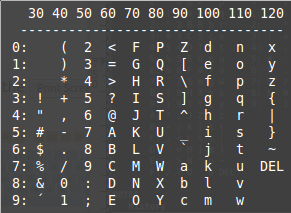
自分であいさつをするプログラムを書いてみよう。
7つある算術演算子。スタックにある整数に対して演算をして、その結果 をスタックへ出力。
+ - * / mod /mod */
mod は、余り。/mod は、商と余り。*/ は、分数。
12 253 + . 265 ok 265 12 - . 253 ok 365 7 / . 52 ok 366 7 mod . 2 ok 366 7 /mod . . 52 2 ok 365 2 3 */ . 243 ok
3分の2を計算するには、*/ をつかえばいい。
次のヒントをもとに、gforthで実行してみよう。
1000 2 3 */
1000 2 3 */ までを入力して、Enterキーを押しただけでは、「ok」が返っ てくるだけである。画面には ok しかでないが、Forth のスタックには計算 した結果がスタックの一番上に仕舞われている。
それを画面に表示するには、「.」(ドット)を使う。ドットは、スタックの最 上位を画面に表示し、スタックの最上位を空にする。
1000 2 3 */ .
全部の牛の3分の1の3分の2が70頭だとすると、牛は全部で何頭か?
3分の1の3分の2、すなわち全体の9分の2が70頭なら、全部の頭数は2分の9 を70にかければよい。
分子が1の分数を単位分数という。エジプトでは、すべての分数を異なる単位分 数の和としてあらわした。ただし、3分の2だけは例外であった。
2/9 = 1/x + 1/y
単位分数の分母、xとyを求める。(ヒント) yは、18。
古代エジプトの僧侶アーメスが書き記したパピルスに次のようなものがある。
家 猫 ねずみ 麦 ます 和
7 49 343 2401 16807 19607
この数字は、なにを意味しているのだろうか?
(ヒント)
Forth で次のような計算をやってみて結果が導きだされた過程を考えよ う。次にどのようにすれば、和がえられるか計算式を考えて実行してみよう。
7 7 * .
7 7 7 * .
7 7 7 * * .
7 7 * 7 + .
7 7 7 7 * * * 7 7 7 * * 7 7 * 7 + + + .
アーメスは、7のベキ乗を具体的に計算したのかもしれない。家が7軒、1軒の家には猫が7匹、1匹の猫は7匹のねずみを捕まえ、1匹のねずみは7本の麦を食い、……
しかし、単位が異なるものを加算する「和」に意味があるのかどうかは 無視して計算する。算術の問題を、身近にするために家、猫、ねずみ、麦、 ますと書いたのだろうか?
13世紀のフィボナッチ(ピサのレオナルド)が書いた『算盤書』にも、同 じ問題がある。フィボナッチは、アーメスのパピルスを知っていたのだろう か。
1+
1-
2+
2-
2*
2/
abs
negate
min
max
: difference - abs ;
52 37 difference 15 ok
37 52 difference 15 ok
家具セールスマンの手数料
: commission 10 / 5000 min ;
60000 commission . 5000 ok
30000 commission . 3000 ok
1500 commission . 150 ok
do ... loop
どのコンピュータ言語も、手続を何度か反復する命令を持っている。do ... loop も同じく「...」を繰り返す。次の例の 10 0 do ... loop の10 は「上限値」、0は「指標(インデックス)」と呼ぶ。インデックスの値を0 からスタートし10に向って「0,1,2,3,4,5,6,7,8,9」と1ずつ増やしながら「...」 を繰り返し、10になるまでの間は反復して実行する。
: test 10 0 do cr ." Hello! " loop ;
test
hello!
hello!
hello!
hello!
hello!
hello!
hello!
hello!
hello!
hello! ok
次のワード定義 decade は、0 からはじめて 10回ループする。ループ制御 は、do と loop で囲まれた「 i . 」を反復する。反復回数は、リターンス タックの一番上で数える。そのリターンスタックの一番上を取り出し、デー タスタックに入れる役目をはたすのが 「 i 」である。
i の値は、ループごとに1増加する。
: decade 10 0 do i . loop ; decade 0 1 2 3 4 5 6 7 8 9 ok
リミットとインデックスは、それぞれ自由にセットできる。
: sample -243 -250 do i . loop ; ok
sample -250 -249 -248 -247 -246 -245 -244 ok
次のワード kake 定義では、 n kake で、nを2倍、3倍、... にする。
: kake cr 11 1 do dup i * . loop drop ; ok
7 kake
7 14 21 28 35 42 49 56 63 70 ok
3 kake
3 6 9 12 15 18 21 24 27 30 ok
もしも金利が6%あれば
R% は、四捨五入をする。
1000円を年利6%で預けるたとき、毎年の預金額は 1000 6 compund で計 算される。
: R% 10 */ 5 + 10 / ;
: COMPOUND ( amount interest -- )
CR SWAP 21 1 DO ." YEAR " I . 3 SPACES
2DUP R% + DUP ." BALANCE " . CR
LOOP 2DROP ;
1000 6 compound YEAR 1 BALANCE 1060 YEAR 2 BALANCE 1124 YEAR 3 BALANCE 1191 YEAR 4 BALANCE 1262 YEAR 5 BALANCE 1338 YEAR 6 BALANCE 1418 YEAR 7 BALANCE 1503 YEAR 8 BALANCE 1593 YEAR 9 BALANCE 1689 YEAR 10 BALANCE 1790 YEAR 11 BALANCE 1897 YEAR 12 BALANCE 2011 YEAR 13 BALANCE 2132 YEAR 14 BALANCE 2260 YEAR 15 BALANCE 2396 YEAR 16 BALANCE 2540 YEAR 17 BALANCE 2692 YEAR 18 BALANCE 2854 YEAR 19 BALANCE 3025 YEAR 20 BALANCE 3207
四捨五入のアルゴリズム
rounded up
: r% 10 */ 5 + 10 / ;
227 32 r% . 73 ok
+loop を使えば、2以上ずつ増やすこともできる。次のgogoは、5ずつ増 やす。
: gogo 50 0 do i . 5 +loop ; ok gogo 0 5 10 15 20 25 30 35 40 45 ok
1ずつ減らすことも +loop でできる。
: falling -10 0 do i . -1 +loop ; ok falling 0 -1 -2 -3 -4 -5 -6 -7 -8 -9 -10 ok
方程式を入力する。
a x^2 + b x + c
演算子 パラメータ リターン
スタック スタック
a b c x
>R a b c x
SWAP ROT c b a x
R@ c b a x x
* c b ax x
+ c ax+b x
R>* c x(ax+b)
+ x(ax+b)+c
: QUADRATIC ( a b c x -- n ) >R SWAP ROT R@ * + R> * + ;
2 7 9 3 quadratic . 48 ok
3.141 ... = 355/113 中国 祖沖之(5世紀)
223/71 <π<22/7 アルキメデス(紀元前3世紀)
3.141 ... = 1068966896 / 340262731
1.414 ... = 19601 / 13860
1.732 ... = 18817 / 10864
2.718 ... = 28667 / 10546
√10 = 3.162 ... = 22936 / 7253
整数による分数で、小数点以下の数値を計算したあと、小数点の適当な位置を決めればよい。
35500000000 113 / .Lua
print(355/113)
摂氏、華氏、ケルビン温度は、次の公式でそれぞれ変換することができる。
°C = (°F - 32) / 1.8 °F = (°C × 1.8) + 32 °K = °C + 273

https://upload.wikimedia.org/wikipedia/commons/a/a0/Lord_Kelvin_photograph.jpg
Forth または Lua で、次の変換を計算する式とその結果。0°F は、摂氏何度か 100°Fは、摂氏何度か 212°Fは、摂氏何度か -32°Fは、摂氏何度か 18°Cは、華氏何度か 233°Kは、摂氏何度か
: F>C 32 - 10 * 18 / ;
: F>K ;
: C>F ;
: C>K ;
: K>C ;
: K>F ;
Lua では、°Cから°Fに変換する関数は次のようになる。
function f2c(c)
c = (f - 32) / 1.8
return c
end
f = 0
print(f,f2c(c))
9 9 - 9 9 / . 1 ok
9 9 / 9 9 / + . 2 ok
9 9 + 9 + 9 / . 3 ok
...
lua
print( 9 - 9 + 9 / 9 )
print( 9 / 9 + 9 / 9 )
print( (9 + 9 + 9) / 9)
...
ここまで、Forthによる計算は整数で実行してきた。たとえば、°Fを°C に変換するときの1.8による割り算を、わざわざ18をかけて10で割ること で実行した。
特にふれなかったが、Forthにも浮動小数点で計算する仕組みはもちろんある。
2e0 fsqrt f. 1.4142135623731 ok
浮動小数点表示の数は、2e0や2.0e0などのように指数表示する。四則演算は、 f+ f- f* f/ のように fがつく。さらにスタックも浮動小数点用の専用スタッ クがあり、f. でそのスタックのTOSを画面表示することができる。スタック内 の fswap fdup などの操作もあるが省略する。
古代バビロニアの数学
粘土板タブレットに刻まれた√2を示す数値。60進法であらわしている。La tablette d'argile YBC 7289

粘土タブレットに刻まれた60進法の数字は、次のように解読された。
30 1, 24, 51, 10 42, 25, 35
a = 1 + 24/60 + 51/60^2 + 10/60^3 = 30547/21600 b = 42 + 25/60 + 35/60^2 = 30547/720 c = 30 b = a c
a = 30547/21600 ≒ 1.41421296 √2 ≒ 1.41421356
YBC 7243 には、「Jannuary 24, 51 10, diagonal of the square」の文字 が刻まれていた。この事実からも、辺の長さが30の正方形の対角線を計算した ものであったことが推測される。この30は何か古代バビロニアで意味のあっ た長さかもしれない。
しかし、この粘土タブレットには古代バビロニアでの平方根の計算方法が不明 である。これは推測だがヘロンの方法を使ったのではないかと言われている。 ちみに日本では江戸時代だが筆算による開平法が知られていた。

https://upload.wikimedia.org/wikipedia/commons/2/2e/Hero_of_Alexandria
平方根を求めるやり方は、古代バビロニアからギリシア、ローマ、中世ヨー ロッパを経由して江戸初期の和算家らに伝えられたという説もある。
Sの平方根を求めるバビロニアのやり方。次のアルゴリズムにしたがう。
1. 任意の正数x(0)からはじめる。(Sの平方根に近い数がベター) 2. x(n+1) を x(n)と S/x(n) の平均とする。(算術平均を幾何平均の近似に) 3. ステップ2をくり返す。(必要な精度になるまで)
S = 200000000 x(0) = 15000 x(1) = (x(0) + S/x(0))/2 = (15000 + 200000000/15000)/2 = 14166 x(2) = (x(1) + S/x(1))/2 = x(3) = (x(2) + S/x(2))/2 =gforthによるx(1)の計算
15000 200000000 15000 / + 2 / .lua によるx(1)の計算
print((15000 + 200000000/15000)/2)
Forth, Lua でアルゴリズムを実際に計算につかい確かめる。
: countdown ( n --)
begin cr dup . 1 - dup 0 = until drop ;
5 countdown
5
4
3
2
1 ok
: repeat-until ( n / 2)
begin cr dup . 2 / dup 0 = until drop ;
1024
512
256
128
64
32
16
8
4
2
1
: rectangle 256 0 do i 16 mod 0= if cr then ." *" loop ;
rectangle を定義して、次のように page rectangle を実行してみる。
page rectangle
: test 0 = invert if cr ." ゼロとちがう!" then ;
0 test ok
12 test
ゼロとちがう! ok
GForth には、2つゲームプログラム(tt.fs, sokoban.fs)がある。テトリスと 倉庫番で遊ぶことができる。ただし、アスキー文字。壁(#)、ゴール(.)、荷物($)、倉庫 人(@)などの文字を見て想像しながらゲームする。ゲームプロブラムの場所は、 インストールしたOSによって異なる。
gforth tt.fs
gforth sokoban.fs
Level: 1 Score: 0 Moves: 0 Rocks: 6
#####
# #
#$ #
### $##
# $ $ #
### # ## # ######
# # ## ##### ..#
# $ $ ..#
##### ### #@## ..#
# #########
#######
ASCII-maps
# wall
. goal
$ packet
* packet in goal
@ Pusher
+ Pusher on goal
sokoban.fs で最初の画面をクリアすると、次の順番で倉庫がでてくる。
2.
############
#.. # ###
#.. # $ $ #
#.. #$#### #
#.. @ ## #
#.. # # $ ##
###### ##$ $ #
# $ $ $ $ #
# # #
############
3.
########
# @#
# $#$ ##
# $ $#
##$ $ #
######### $ # ###
#.... ## $ $ #
##... $ $ #
#.... ##########
########
整数が二つあるとき。二つとも割り切る正の数を公約数という。公 約数のうち最大のものを最大公約数という。二つの整数を a、bとするとき、 もしbがaを割り切るならば、aとbの最大公約数はbである。
整数 a,b の最大公約数を求める。
1. a を b で割り、余りを r とする。(0 ≦ r < b)
2. もし、r=0 ならば b が最大公約数である。
3. a ← b, b ← r とし、1 に戻る。
プログラム
: gcd ( a b -- n )
begin dup while tuck mod repeat drop ;
544 119 gcd .
例をあげてみよう。1からはじまる奇数の和を計算する簡単な式が予想でき る。
1 = 1の2乗 1+3 = 2の2乗 1+3+5 = 3の2乗 1+3+5+7 = 4の2乗 1+3+5+7+9 = 5の2乗
そこで一般的な法則をたてる。
1+3+ ... +(2n-1) = nの2乗
このnについての一般的な式をP(n)としよう。P(n)がすべての整数nにつ いて成り立つことを証明できるだろうか。
1+3+...+(2n-1)+(2n+1)=nの2乗+2n+1=(n+1)の2乗 となって、
P(n+1)が成立する。(証明終り)
インドを源流とした数学がアラビアで代数の形式の基礎を得ることができ、 それは16 世紀のイタリアで開花した。17世紀数学は、古代ギリシアの数学 の成果を再評 価するすることにもなる。それはフランスとイギリスで成長 し現代数学の 一分野微積分の誕生へとつながった。微積分は、さらに高い レベルへ抽象化がすすみ、虚数の概念の理解がすすみ解析学から複素解析学 へと発展していく。それには、18世紀の数学者、スイス人やドイツ人であり ながらヨーロッパ大陸をわたり歩いた汎ヨーロッパ的な数学者がいたことを 示す。
スイスのバーゼルには、優秀な数学者を輩出したベルヌーイ一族がいた。 ライプニッツの著作で学んだヤコブ・ベルヌーイは、あたらしい数学の分野で ある微積分を拡張 した。ライプニッツが使っていた calculus summatoriusという言葉を calculus integralisという言葉に置き換えたのは、ヤコブ・ベルヌーイであっ た。これが「積分」という用語の誕生であった。
ヤコブは、整数の逆数の和が発散することを証明した。さらに、整数の2乗 の和は収束することを示したが、その値はもとめていない...
1 + 1/2 + 1/3 + 1/4 + ...

ウイキメディアコモンズよりヤコブ・ベルヌーイ
ベルヌーイ一族のダニエルは、数学を流体力学に応用したパイオニアであっ た。 Daniel Bernoulli - Hydrodynamics
ヨーロッパでの王立アカデミー。ライプニッツの働きかけ。
研究は、科学と数学。
フランス王立アカデミー ロシア王立アカデミー プロイセン王立アカデミー
ウィキメディアコモンズよりサンクトペテルブルグの位置
1725年にダニエルとニコラスのベルヌーイ兄弟がサンクトペテルブルクのロ シア王立アカデミーへ招待された。兄弟は、ふたりとも確率論に興味があり、 数学的期待値の理論にとりくんだ。
数学的期待値について説明しておこう。ある投資で1000万円もうかる確率が50 パーセント、200万円失う確率が50パーセントだとしよう。この投資は、どの くらいの価値があるだろうか?確率の法則では、それぞれの金額と確率をかけ て、総和を計算すれば期待値がもとまる。
1000万円・0.5 + (ー200万円)・0.5 = 400万円
数学的期待値は、この投資をくり返したときの合理的かつ長期的な結果を示し ている。何度も試行をくり返してあとで平均すれば400万円もうかるというこ とだ。
ベルヌーイ兄弟のダニエルとニコラスは、ここであるストーリーを考えた。そ れをすこし現代風にすると次のようになる。
胴元がひとりのプレーヤを相手にしたコイン投げのゲームをやるとしよう。 かけは、2百円からはじめる。コンイのオモテがでるたびに賞金は倍々になってゆ く。ウラがでるとゲームはおわり、プレーヤの勝ちで賞金を全部と ることができる。したがって、1回目でウラがでたらプレーヤは2百円もらう。 オモテが1回目にでて2回目にウラがでるとプレーヤは4百円もらう。オモテ が2回つづけてでて3回目にウラがでるとプレーヤは8百円もらう。3回つづけ てオモテがでて4回目にウラがでたときは1千6百円もらうことになる。こうやっ て、プレーヤが手にする金額は2のK乗の百倍になる。ここでKは、コインを投げた 回数である。さて、胴元はゲーム参加費をいくらにすれば公平なゲームになるだろ うか。というのが問題である。
コインのオモテとウラのでる確率が 1/2 のとき2百円、 1/4のとき4百円、1/8 のとき8百円、…… であるから、期待値は、
期待値(百円単位) = 1/2・2 + 1/4・4 + 1/8・8 + 1/16・16 + …
= 1 + 1 + 1 + 1 + …
= ∞
このゲームは、オモテがでる限り続くことになるから胴元は天井なしの資金を用意 しなければ期待値無限大にこたえることができない。これは現実的で はない。
実際にやってみると、平均で500円未満になる。もし、参加費が3000円だ とすると、現実には参加する人はいるだろうか?
このパラドックスをきっかけに、ベルヌーイ兄弟は、実際の期待値と「数学的 期待値」を区別するようになった。
実際の期待値は、金とリスクに対する人間の態度によるということだ。リスク を回避するか、リスクを求めるかである。

ウィキメディアコモンズよりダニエル・ベルヌーイ

ウィキメディアコモンズよりニコラス・ベルヌーイ
何人集れば、そのなかに同じ誕生日の人がいる確率が50%を超えるか?
この問題を解く前に準備をする。ある人の誕生日が自分と同じ確率はいく らか。答は、1/365である。 したがって、ある人の誕生日が自分と異なっている 確率は364/365 = 1 - 1/365 である。ある部屋に自分をふくめて12人いる場 合の確率を計算してみよう。自分以外の11人 について誕生日が自分と異なる確率は、11人について全部同じ364/365である。 だから11人すべての誕生日 が自分と違う誕生日である可能性は、 (364/365)*(364/365)*(364/365)*(364/365)*(364/365)*(364/365)*(364/365)*(364/365)*(364/365)*(364/365)*(364/365) = (364/365)^11 = 0.97...
これは自分と同じ誕生日の人が一人もいない確率である。「一人もいない」 の否定は、「少くとも一人いる」である。したがって、自分と同じ誕生日の人が少くと も一人いる確率は、1 - 0.97... = 0.03... となり、3%とかなり小さい。 12人を倍まで増やしても、とても50%にはなりそうにない。
しかし、ここまでの推論は間違っている。
誕生日問題で計算する確率は、「自分と同じ誕生日の人が同じ部屋にいる 確率」ではなく 「同じ部屋に同じ誕生日の2人(ペア)がいる確率」だ。
部屋のなかにいるn人で、1ペアをつくる組み合わせは n(n-1)/2 通りあ る。部屋のなかの人数n が増えていくと、nの2乗で組み合わせの数は増える ことに着目しよう。人数が増えると、誕生日の組み合わせは2乗で増える。
それでは「同じ部屋に同じ誕生日の人間がいない、すなわち全員の誕生日が異 なる確率」を計算しよう。12人すべての誕生日が異なっている確率は、
(364/365)*(363/365)*(362/365)*(361/365)*(360/365)*(359/365)*(358/365)*(357/365)*(356/365)*(355/365)*(354/365) = 0.83...
となる。12人全員の誕生日が異なっている確率が、0.83であるから、誰か が同じ誕生日を共有している確率は、1-0.83 = 0.17 となる。
12人のうち誕生日が同じものがいる確率が0.17となった。それでは、倍の 24人ではどうなるだろうか。24人すべての誕生日が異なっている確率を計算 すると、0.46となることから、誰かが同じ誕生日である確率が 0.54で50 %を超えているため、23人と22人で確率を計算しなおす。すると23人では 51%、22人では48%となった。したがって、23人を超えたところで、同 じ誕生日のものがいる確率の方が、いない確率よりも高くなることがわかる。
雑誌サイエンティフィック・アメリカンの2014年2月号に掲載された記事 「Math Explains Likely Long Shots, Miracles and Winning the Lottery」 をもとに「大数の法則」と「組み合わせの法則」について考える。
「01」から「43」までの43個の数字のなかから6個を選んで購入する。1 等は、6個の数字すべてが一致したとき。
43 42 41 40 39 38 * * * * * 6 / 5 / 4 / 3 / 2 / . 6096454 ok
ロト6は、日本で実際に行われている数字選択式の宝くじ(ロト)だが、ロ トは世界中で行われている。さきほどのサイエンティフィック・アメリカン には偶然とは信じ難い当りがブルガリアであった事実が載っている。2009年 9月6日に「4、15、23、24、35、42」という当選番号がでた。驚きはその4日 後にまったく同じ「4、15、23、24、35、42」という当選番号が発表された ためメディアは大騒ぎになった。
果たして、これは偶然といえるのだろうか。
ブルガリアのロトは、49個の数字から6つを選ぶ方式なので、ある数字の組 み合わせが選ばれる確率は、
49 48 47 46 45 44 * * * * * 6 / 5 / 4 / 3 / 2 / . 13983816 ok
である。さきほどの「4、15、23、24、35、42」が選ばれる確率は、1398万8316分 の1である。したがって3日間で2回抽選があったとして、その2つの当選番号が一致す る確率は、1398万8316分の1だ。しかし、もしも50回抽選があったとすれば2つ の当選番号が一致する確率はいくつになるだろうか?組み合わせの数を計算す る。n回の抽選をしたとき、そのうちで2つの当選番号が一致する組み合わせは、
n×(n-1)/2組ある。
したがって、50回だと1,225通りあることになる。さらに、1000回だと499,500 通りもある。抽選回数を20倍にすれば、場合の数は407倍にもなるのだ。
まさに「大数の法則」がはたらくことになっていく。
さて、ロトで同じ6つの数が当選する確率が50%を超えるには何回抽選 をやればいいのだろうか?答は4404回となる。
1年間は、52週だから、週2回抽選があれば43年間で4404回を超える。世界中を 考慮すれば4404回を超えるのは1年もかからない。ロトの抽選器が同じ番号を 出すことが50%以上の確率になってしまうのだ。
アルゴリズムは、記号だけで単純化して示す。プログラムは、ことわら ないかぎり GForth で書いたものを示す。
1 1 2 3 5 8 13 21 34 55 89 ...
詳細は、各種整数列オンライン百科事典のOEIS A000045にある。
アルゴリズム
F(1) = 1
F(2) = 1
F(n) = F(n-1) + F(n-2)
プログラム
: fib ( n -- fib )
0 1 rot 0 ?do over + swap loop drop ;
参考として Swift 言語で書いた、フィボナッチ数列を1項から30項まで計 算するプログラムを次に示す。1から7行は、関数(func)の定義である。関数 名は fibonacci 、引数として 整数(Int) n をあたえれば、その結果を整数 で返す( -> Int)。
func fibonacci(n: Int) -> Int {
if n < 2 {
return n
} else {
return fibonacci(n-1) + fibonacci(n-2)
}
}
for i in 1...30 {
print(fibonacci(i))
}
(解説)
フィボナッチ(ボナッチの息子)は、イタリア、ピサのレオナルド(1170頃ー 1250)という人物。数学者として何冊も本を書いた。そのうちの1冊『算盤の書』は、19世紀になってもヨーロッパの主要な数学のテキストであった。
正の整数で、自分自身の約数の和が自分自身になる数。ただし、自分自身 は約数にふくめない。
アルゴリズム
プログラム
: perfect? ( n -- ? )
1
over 2/ 1+ 2 ?do
over i mod 0= if i + then
loop
= ;
下表のようにある操作を反復すると「1」に収束する数、1や7などがあ る。これを幸運の数という。残りの2や3などは、ある数列のパターンを無 限に繰り返す。これを不幸の数という。
1
2, 4, 16, 37, 58, 89, 145, 42, 20, 4, 16, 37, 58, ...
3, 9, 81, 65, 61, 37, 58, 89, ...
4, 16, 37, 58, ...
5, 25, 29, 85, 89, 145, ...
6, 36, 45, 41, 17, 50, 25, 29, 85, 89, 145, ...
7, 49, 97, 130, 10, 1
...
参考プログラム
: next ( n -- n )
0 swap begin 10 /mod >r dup * + r> ?dup 0= until ;
: cycle? ( n -- ? )
here dup @ cells +
begin dup here >
while 2dup @ = if 2drop true exit then
1 cells -
repeat
1 over +! dup @ cells + ! false ;
: happy? ( n -- ? )
0 here ! begin next dup cycle? until 1 = ;
: happy-numbers ( n -- )
0 swap 0 do
begin 1+ dup happy? until dup .
loop drop ;
8 happy-numbers
ルーン・アルゴリズムあるいはルーン・テストと呼ばれている計算式は10で割 り算したあまりを求めて、簡単なチェックを行なう。クレジット・カード番号 、携帯電話の識別番号(IMEI番号)、米国医療機関識別番号、カナダ社会保証 番号などで使われている。
もとは、50年以上前にIBMの科学者が特許をとったものである。現在はパブリッ クドメインで公開され広く利用さている。ランダムな数字列から識別番号を選択するときのチェックに使われる。
ウィキペディアに識別番号が49927398716の検証例がある。
アルゴリズム
例として、49927398716についてチェックを実行する。
まず、数字の並びを反転させる: 61789372994 奇数けたの数を足す。 6 + 7 + 9 + 7 + 9 + 4 = 42 = s1 偶数けたの数について: 1, 8, 3, 2, 9 それぞれを2倍する: 2, 16, 6, 4, 18 それぞれの積について、数字を足す: 2, 7, 6, 4, 9 その合計を求める: 2 + 7 + 6 + 4 + 9 = 28 = s2 s1とs2の和を求め、ゼロで終っていれば合格。 s1 + s2 = 70 これが、ルーン テスト。
プログラム
: luhn ( addr len -- ? )
0 >r over + ( R: sum )
begin 1- 2dup <=
while \ odd
dup c@ [char] 0 -
r> + >r
1- 2dup <=
while \ even
dup c@ [char] 0 -
2* 10 /mod + \ even digits doubled, split, and summed
r> + >r
repeat then
2drop r> 10 mod 0= ;
実際にルーンテストをgforthでターミナル画面などで実行する手順は次のようになる。最初に上のプ ログラムをエディタ等で書いて名前を付けファイルに保存する。例ではファイ ル名を「luhn-test.fs」としている。「$」は、Windowsなどでのターミナル画 面でユーザ入力を待つプロンプトである。
プロンプト$のあと、gforth luhn-test.fs をターミナル画面で入力すると gforth は、プログラムファイル luhn-test.fs を読み込みユーザからの命令 を待つ。
$ gforth luhn-test.fs Gforth 0.7.3, Copyright (C) 1995-2008 Free Software Foundation, Inc. Gforth comes with ABSOLUTELY NO WARRANTY; for details type `license' Type `bye' to exit s" 49927398716" luhn . -1 ok
「Type `bye' to exit」の次の行に、チェックしたい認識番号と数字列の長さ を入力する。それが、「s" 49927398716"」までである。Forthでは、s" ..." によって「...」の列がその列が収納された記憶装置の番地と列の長さの2つの 要素に分解されて、スタックに格納される。
したがって、s" ..." につづいてワードluhnを入力すればluhn-test.fsファイ ルの中で定義されたワードluhnが呼び出されて実行される。
-1と出力されると合格である。0は、不合格。
(参考)Lua によるルーンテストのプログラム
function luhn(n)
n=string.reverse(n)
print(n)
local s1=0
--sum odd digits
for i=1,n:len(),2 do
s1=s1+n:sub(i,i)
end
--evens
local s2=0
for i=2,n:len(),2 do
local doubled=n:sub(i,i)*2
doubled=string.gsub(doubled,'(%d)(%d)',function(a,b)return a+b end)
s2=s2+doubled
end
print(s1)
print(s2)
local total=s1+s2
if total%10==0 then
return true
end
return false
end
-- Note that this function takes strings, not numbers.
-- 16-digit numbers tend to be problematic
-- when looking at individual digits.
print(luhn'49927398716')
print(luhn'49927398717')
print(luhn'1234567812345678')
print(luhn'1234567812345670')
ルーンチェックは、クレジットカードなどのように一見するとランダムな 数字列について、不正な識別番号を選別するために用いられる。学籍番号の ようにクレジットカードのシステムと異なるものは、ルーンチェックでは 「0」が出力されるはずである。
ジニ係数(ジニけいすう、英: Gini coefficient)とは、主に社会におけ る所得分配の不平等さを測る指標。
ピケティ『21世紀の資本論』を読む。「拡大する貧富の格差」「市場のダ イナミズム優先か、それとも再配分か」。日経BPまとめ読みサイトへのリンク。
THE WORLD FACTBOOK (CIA) : COUNTRY COMPARISON :: DISTRIBUTION OF FAMILY INCOME - GINI INDEX